Mijn naam is Lieselotte en ik ben developer bij Inergy. Elke dag programmeer ik voor toffe projecten bij verschillende klanten. Ik spijker mijzelf continu bij op wat meer algemene basis kennis van de IT. Aangezien onze slogan luidt: “Let’s play create and grow together”, dacht ik: “OK! Let’s learn together”. Of je nu net als ik nieuwsgierig bent naar IT onderwerpen zoals een algoritme, of dat je wel houdt van een recap momentje, lees dan lekker verder.
In mijn vorige blog schreef ik over het Breadth-first-search algoritme. In deel 2 van de serie Let’s learn about algorithms kijken we naar het Dijkstra-algoritme. Lees snel verder om meer te weten te komen over het Dijkstra-algoritme en hoe dit algoritme verschilt van het Breadth-first search-algoritme.
Dijkstra algoritme
Naast het Breadth-first-search algoritme zijn er veel meer algoritmes die hetzelfde soort probleem “Wat is de snelste weg van A naar B”? proberen op te lossen. Afhankelijk van de specifieke situatie zal het ene algoritme een betere keuze zijn dan het andere.
In ons eerste voorbeeld hadden de connecties (wegen) geen waarde, maar er zijn natuurlijk heel veel vraagstukken waar de wegen wel een waarde hebben. Denk bijvoorbeeld aan het uitstippelen van de snelste route van Woerden naar Amsterdam. Dan hebben de wegen die je kunt volgen een bepaalde afstand of duurt het een bepaalde tijd. Wanneer er een waarde aan de wegen wordt gegeven is het Breadth-first-search algoritme niet meer toereikend. Het Breadth-first-search algoritme zal je het pad geven met het minst aantal stappen, wat niet altijd gelijk staat aan het kortste of het snelste pad.
Voor zo’n probleem heb je het welbekende Dijkstra Algoritme nodig. Oke, laten we kijken hoe het algoritme in zijn werk gaat. We beginnen met een makkelijk voorbeeld, we willen zo snel mogelijk van thuis naar het café komen.
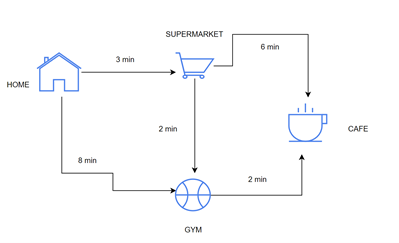
We beginnen bij het huis en schrijven alle informatie die we op dat moment weten op in een tabel. Hierin schrijven we het begin en eind punt op van de wegen die we zien. Voor het café weten we nog niet het pad en ook nog niet de tijd.

We kiezen ervoor om naar het dichtstbijzijnde punt te gaan, de supermarkt. Eenmaal aangekomen zien we dat de gym maar 2 minuten van ons vandaan is en het café nog 6 minuten. Met deze nieuwe informatie weten we dat gym sneller bereikbaar is via de supermarkt. We gaan de tabel updaten.
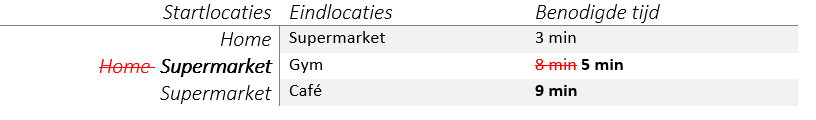
We gaan weer verder naar het volgende goedkoopste punt, de gym. Hier zien we dat het café nog 2 minuten verder lopen is. We komen er nu achter dat het café sneller bereikbaar is via de gym dan rechtsreeks vanaf de supermarkt. We werken de tabel weer bij.
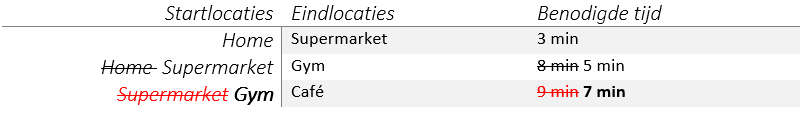
Nu we alle punten hebben gehad, weten we dat snelste weg naar het café 7 minuten duurt. Om de route terug te vinden start je bij de eindlocatie en volg je tabel terug via de start locaties. Café à Gym, Gym à Supermarket, Supermarket à Home.
Alle stappen samengevat
Je zou wat we net hebben doorlopen kunnen omschrijven in een paar stappen:
- Kies het dichtstbijzijnde punt.
- Aangekomen op het nieuwe punt, werk de tijden bij met de nieuwe info die je hebt. Werk alleen de tijden bij als het sneller is dan de info die er stond.
- Herhaal stap 1 en 2 tot dat je dit voor elk punt hebt gedaan.
- Lees het snelste pad terug in de tabel.
Het Dijkstra algoritme in code
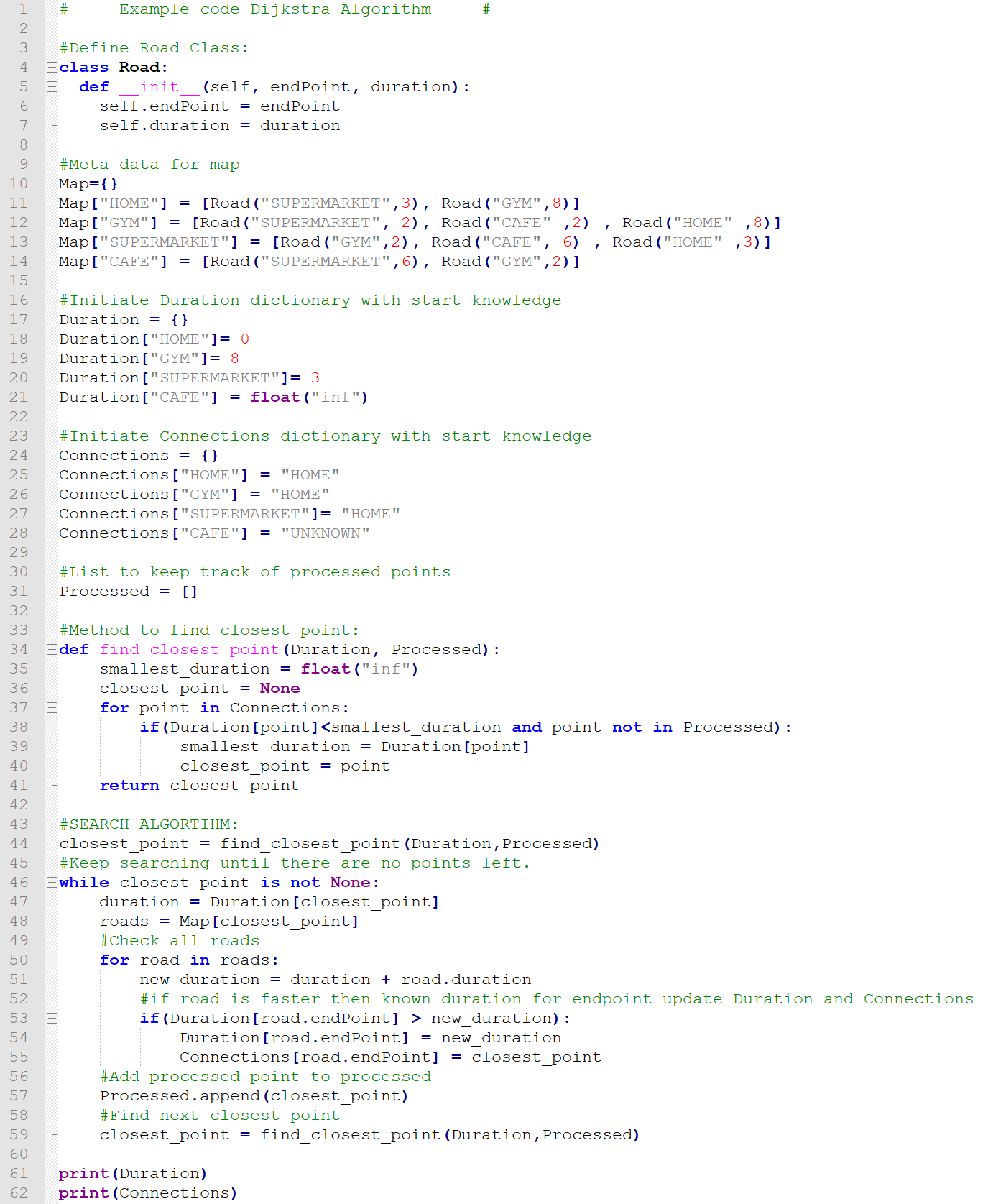
Oké, laten we dit algoritme proberen op te schrijven in een stukje code. Stuur ons gerust een e-mail als je deze code in tekst wil ontvangen:
Verschillende situaties testen
Nu we het stuk code hebben geschreven kunnen we allerlei situaties gaan testen. Om zeker te weten dat we het Dijkstra algoritme goed snappen moeten we onszelf afvragen wat het algoritme doet onder verschillende omstandigheden. Welk pad geeft het algoritme als twee of meer paden even lang zijn? Of hoe gaat het Dijkstra algoritme om met negatieve waardes?
Stel je voor dat de weg tussen de supermarkt en de gym niet 2 minuten duurt, maar 4 minuten?
Dan is de weg Home –> Supermarkt –> Gym –> Cafe, even snel als Home –> supermarkt –> café.
Welk pad is de uitkomst van het Dijkstra algoritme?
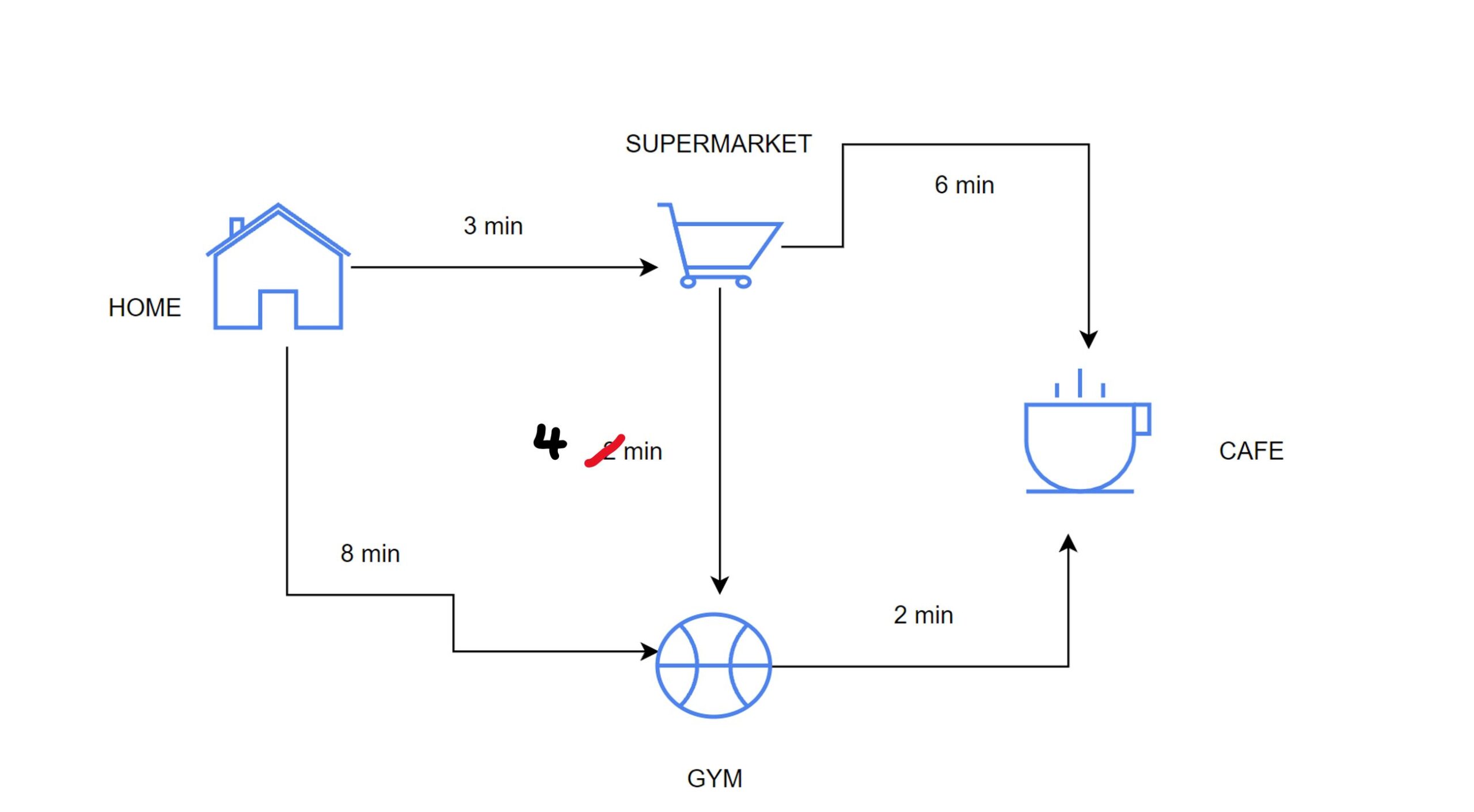
Het algoritme gaat altijd eerst naar het dichtstbijzijnde punt, in ons voorbeeld de supermarkt. Op dit moment update hij de tijd van het café van oneindig naar 9 minuten met als pad via de supermarkt. Daarna gaat het algoritme door naar de GYM, hier update hij de tijd en het pad van het café NIET, omdat het pad niet sneller is dan het pad dat hij eerder had gevonden. De volgorde waarop het algoritme door de punten gaat is dus belangrijk voor het resultaat.
Laten we nu een gedachte-experiment doen voor negatieve waardes. Neem dit simpele voorbeeld met 4 punten en 4 wegen, we gaan van punt A naar punt D. Wat is de snelste weg volgens Dijkstra?
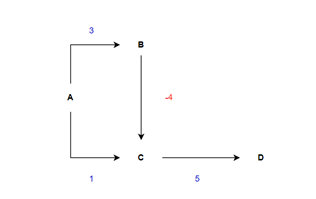
Beginsituatie in de tabel opgeschreven:

Stap 2: ga naar dichtstbijzijnde punt –> C. Werk de tabel bij.

Stap 3: ga naar het volgende dichtstbijzijnde punt –> B. Hier zien we dat er een goedkopere manier is om naar punt C te komen, terwijl we punt C al hadden bekeken! We updaten de tabel weer.

Zoals jullie zien gaat het hier fout. Het eindresultaat is 6, terwijl er een pad is voor maar 4. Dit komt omdat het algoritme er vanuit gaat dat wanneer hij een punt heeft gehad, dit de laagste waarde voor het punt is. Bij negatieve waardes is dit niet het geval, daarom is het Dijkstra algoritme niet bruikbaar voor problemen met negatieve waardes. Ga zelf eens opzoek naar een algoritme die wel om kan gaan met negatieve waardes.
Samengevat
Samenvattend, in deze blog serie hebben we twee verschillende algoritmes bekeken die een oplossing bieden voor het snelste pad bepalen tussen punt A en B. Het Breadth-first search algoritme resulteert in een pad met het minst aantal stappen, zoals we zagen in het voorbeeld van de developer die we zochten in onze connecties. Daarentegen beantwoord het Dijkstra algoritme de vraag met het goedkoopste pad. Beide algoritmes zijn erg interessant omdat ze toepasbaar zijn op verschillende soorten vraagstukken.
Natuurlijk hebben we nog lang niet alles besproken wat erover deze algoritmes te vertellen valt, maar voor nu wil ik het hier bij laten. Ik hoop dat jullie dit een leuke blog vonden om te lezen, zo ja kijk dan uit naar mijn volgende blog!




